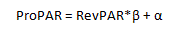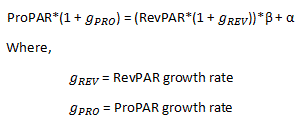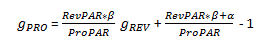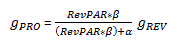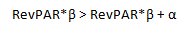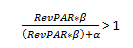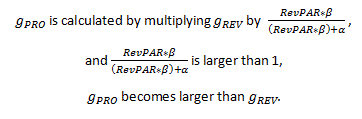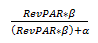ProPAR Graph
Earlier this year, Hotel Appraisers & Advisors published an article summarizing how several hundred hotels performed, ranked by House Profit per available room (ProPAR). The article then compared each hotel’s ProPAR level relative to Rooms Revenue per available room (RevPAR). By standardizing for RevPAR, the analysis allowed us to compare profitability of hotels of different service types, chain scales, and brands. This metric also allows owners to compare the performance of hotels managed by different management companies. By using ProPAR and RevPAR, HA&A showed a simple way of analyzing hotel profitability, while standardizing all variables that affect revenue.
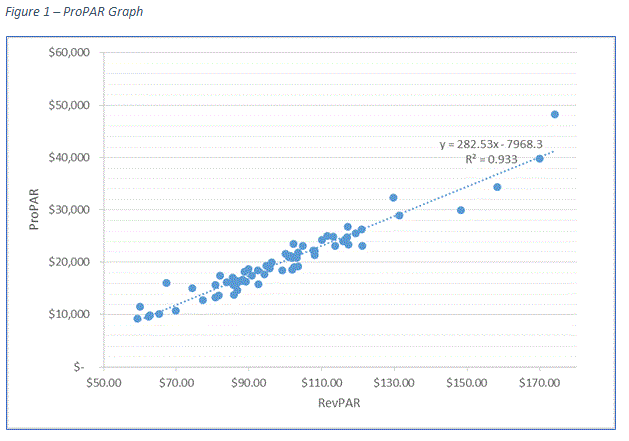
The scatter plot in the ProPAR graph above is constructed by using data of 70 branded, upscale hotels across the county. The scatter plot shows dots gathering tightly along a straight line, which is indicative of a strong linear relationship between RevPAR and ProPAR. This relationship can be expressed mathematically by the following two-variable linear equation:
ProPAR = RevPAR*β + α
In this equation α and β are constants that determine the interception on the y-axis and the slope of the regression line, respectively. In the preceding example, β is 282.53 and α is -7,968.3.
The following figure illustrates how the scatter plot shifted from 2013 to 2014 using the RevPAR and ProPAR data from the sample set.
Since most of the sample hotels experienced positive RevPAR and ProPAR growth between 2013 and 2014, we can see the dots shift in a right-upward direction, from yellow to blue. Yet, the two linear trend lines appear to closely match. This indicates that RevPAR and ProPAR of the sample set maintain their linear relationship regardless of changes in RevPAR and ProPAR levels over time.
In this article, we will illustrate examples of how we can analyze this graph and what we can learn about the relationship between RevPAR and ProPAR.
Deceleration of Profit Growth
The concept of diminishing marginal returns is taught in many micro economics classes. A company’s growth will decelerate as the company matures, or grows, and marginal profits decline. In this section, we show that we can infer a similar relationship between RevPAR and ProPAR from the ProPAR graph.
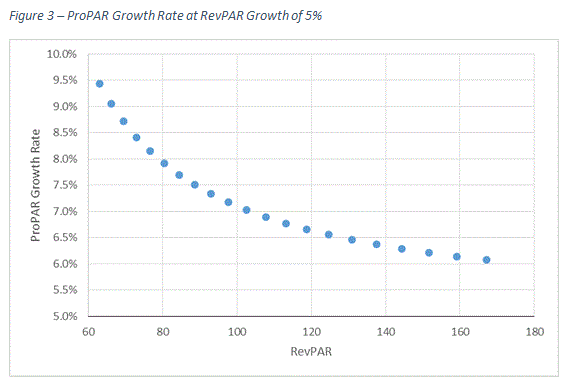
The following figure is created using the linear equation obtained from the earlier ProPAR graph. It shows how ProPAR growth rates change as RevPAR increases by a given amount, say 5.0%. When the RevPAR level is close to $60, ProPAR grew by roughly 9.5% per 5.0% increase in RevPAR. However, when the RevPAR level is close to $170, the ProPAR growth rate decreases to 6.0% per 5.0% increase in RevPAR. This data suggests that ProPAR growth rates decelerate as RevPAR levels increase.
Another noticeable point from Figure 3 is that the decreases in the ProPAR growth rate become smaller as RevPAR levels become larger. At the beginning of the curve, the ProPAR growth rate decelerated by almost 0.5% per 5.0% increase in RevPAR while the ProPAR growth rate decelerated by less than 0.1% near the end of the curve. Is there a point where ProPAR ceases to decrease?
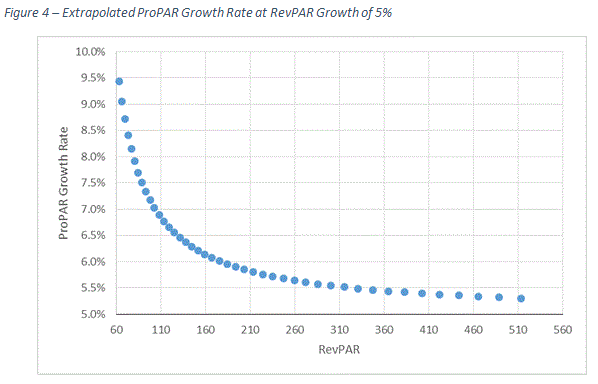
Figure 4 shows what will happen to ProPAR growth if we extrapolate the linear line far beyond our data set. It appears that the ProPAR growth rate is getting closer and closer to 5.0%, which is the RevPAR growth rate intervals we are using in this experiment. As shown later in this article, the curve will “converge” to 5.0% if we assume that we can extend the straight line beyond the data set we sued in our study.
Although the computation of hypothetical ProPAR growth rates loses its relevancy in the real world once RevPAR exceeds realistic levels, the idea that the ProPAR growth rate approaches the RevPAR growth rate has an interesting implication.
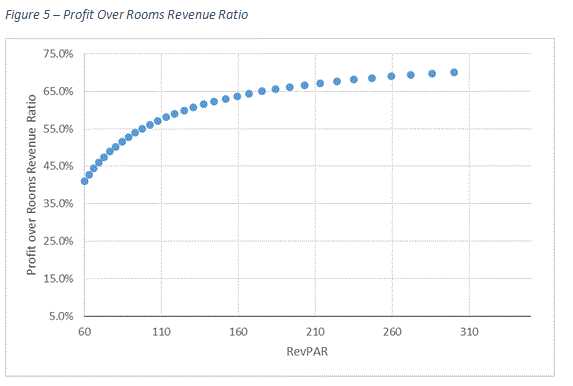
Figure 5 shows how profit margins, expressed as a percentage of rooms revenue, change when RevPAR increases. The curve shows that profit margin growth decelerates as RevPAR levels increase. This is understandable because, as we have illustrated, ProPAR growth rates become smaller as RevPAR levels increase. As ProPAR growth rates converge to the 5.0% RevPAR growth rate, a marginal profit becomes smaller, which stabilizes the profit ratio.
Impact of RevPAR Levels on Profit Growth
In the previous section we illustrated the decelerating nature of profit growth. A major implication of the result is that a hotel’s RevPAR level can help determine the degree to which profit growth can be induced by RevPAR growth.
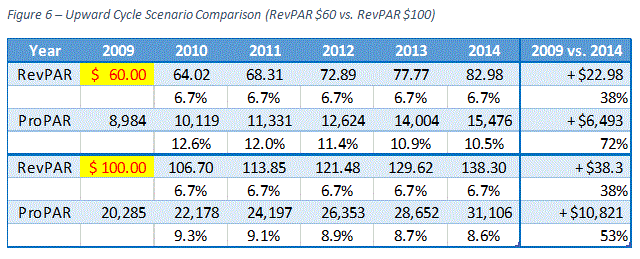
To demonstrate our point in more concrete terms, we have compared two hypothetical scenarios with different RevPAR levels. Between 2009 and 2014, the average hotel in the United States experienced RevPAR growth of approximately 6.7% annually. In our example, we set the beginning RevPAR at $60 for one scenario and $100 for the other. Assuming both hotels experienced 6.7% RevPAR growth annually, which scenario has achieved higher total growth in ProPAR at the end of 2014?
Figure 6 shows that the first scenario with the beginning RevPAR of $60 has increased ProPAR by 72% by the end of 2014, while the second scenario with the beginning RevPAR of $100 has increased ProPAR by 53% over the same period. This is because of the decelerating nature of ProPAR growth illustrated in the previous section.
In reality, however, two hotels with different RevPAR levels may not increase their RevPAR at the same rate. It is possible that the hotel in the second scenario had a higher RevPAR level in the first place because it is located in a better market or is physically in a better condition. If this is true and the hotel is better positioned for an upward cycle, its RevPAR growth could be higher than the first scenario. Then, how much larger the RevPAR growth has to be for the second hotel to have achieved the same ProPAR growth at the end of 2014?
We can compute the percentage by the following calculation:
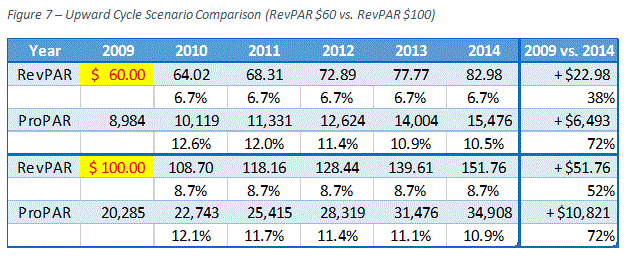
Therefore, total RevPAR growth for the second scenario has to be 35% larger than the first scenario, which equates to 52%. The following figure illustrates two scenarios with the same ProPAR growth percentage at the end of 2014.
The total RevPAR growth rate for the second scenario is increased to 52%, and the total ProPAR growth rate is now 72%, the same as the first scenario. Consequently, this affects the annual growth rate of the second scenario. Comparing the numbers in Figure 6 and 7, the annual growth rates for the second scenario increased by 2.0%.
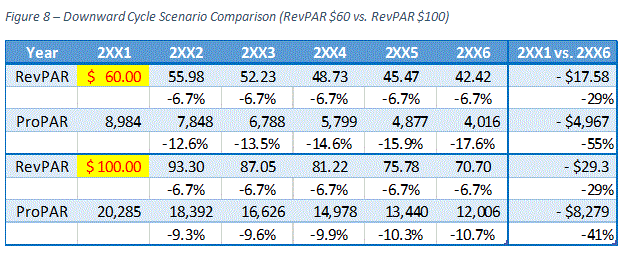
Now, we would like to demonstrate what will happen in case of a downward cycle. In order to make the comparison easier, we have used a negative 6.7% growth rate for our two hypothetical scenarios.
As illustrated in the preceding figure, the scenario with RevPAR of $60 had a larger negative impact than the second scenario with RevPAR of $100. Again, this is because ProPAR growth rate is higher when a RevPAR level is lower, whether the growth rate is positive or negative.
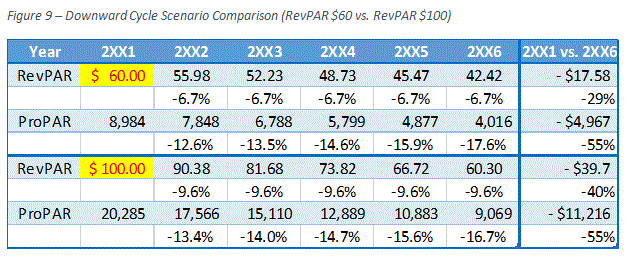
Once again, for the second scenario to have the same level of negative ProPAR growth, RevPAR has to decrease more significantly than the first scenario. Figure 9 shows the second scenario requires -9.6% annual growth to have the same negative impact on ProPAR as the first scenario.
To summarize, we have demonstrated that ProPAR growth rates vary depending on the beginning RevPAR levels, even if we assume RevPAR grows at the same rate. For a hotel with a higher RevPAR level to have the same ProPAR growth rate as a hotel with a lower RevPAR level, its RevPAR has to grow at a faster pace. This is also true for negative growth. In our examples, the second scenario required 2.0% higher annual RevPAR growth rate to have the same ProPAR gain as the first scenario while 3.0% lower annual RevPAR growth rate was necessary to have the same ProPAR loss in the downward cycle.
Mathematical Analysis
In this section, we will mathematically illustrate how the linear relation between RevPAR and ProPAR observed from the ProPAR graph is related to the findings of our experiments.
As previously shown, the ProPAR graph is expressed in the following equation:
With minor alternations to the equation above, we can express how RevPAR growth affects ProPAR growth in the following equation:
Again, our interest is to see an impact of RevPAR growth on ProPAR growth. By shifting everything but g PRO from the left side to the right side of the equation, we will derive the following expression:
Because,
the latter half of the right side of the equation cancels out.
Therefore,
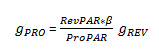
Notice that if the α is zero, the nominator and the denominator will be equal, and the whole fraction becomes one. As a result, g PRO and g REV will be equal. However, since the α represents profitability when RevPAR is zero, the α is always a non-zero, negative number. This is because RevPAR levels need to reach a break-even point to cover fixed expenses before a hotel makes any profit. For this reason, the following expression is true:
And therefore,
From the expression above, it should be clear why ProPAR growth rates are constantly higher than RevPAR growth rates in theory.
Because
Now, let’s see why ProPAR growth decelerates as RevPAR increases. The key here is to remember the α is a constant. As illustrated above,
will never be one. However, as RevPAR increases, the α becomes smaller and smaller relative to RevPAR*β. As a result, as RevPAR gets larger and larger, the whole expression becomes closer to one.
To make this point clear, we will go back to the two scenarios with $60 and $100 RevPAR levels. Plugging in these two different RevPAR levels, we calculate the following:
Concluding Thought
In this article, we have demonstrated what we can learn about the linear relationship between RevPAR growth and ProPAR growth from the ProPAR graph. Our findings indicate that a degree of an impact from RevPAR growth on profit growth varies depending of the levels of RevPAR. An implication from the finding is a subtle, but interesting one. In order to gain a clear understanding of the relationship between RevPAR and profitability, it is essential for us to view RevPAR growth in context of specific RevPAR levels. Talking about RevPAR growth without a specific RevPAR in mind could lead to an inaccurate conclusion for potential profitability of a hotel. For intelligent investment decisions, it is important to have an accurate picture of how RevPAR performance will translate to profitability, and we have shown that the ProPAR graph can be a great tool for the analysis.
This article is intended to present examples of what we can learn from the ProPAR graph. We hope the findings shared in this article attract more interest and encourage further discussion in the industry. We welcome participation from additional management companies and ownership groups who are interested in receiving confidential benchmarking feedback based on our analysis model.